


4 Vérification de modèles
Dans les logiques de la sorte que nous avons décrite en
section 3, le problème de la satisfiabilité ou
celui de la validité ne sont pas aussi importants que dans d'autres
logiques. Une formule F dans ces logiques L est une spécification d'une propriété souhaitée d'un programme.
Les réalisations sont des systèmes de transitions (des programmes
CCS ou des diagrammes états-transitions pour le matériel par
exemple), autrement dit ce sont des modèles (des cadres et
des affectations de Kripke). Vérifier la satisfiabilité d'une
telle formule signifie chercher s'il est possible de réaliser cette
spécification. Bien que ceci soit utile, ce n'est pas réaliste en
général, parce que cela demande que le vérificateur de
satisfiabilité invente un programme réalisant la spécification.
Le vrai problème auquel on est usuellement confronté est le
suivant : étant donnée une spécification d'un système (sous
forme d'une formule modale F), et une réalisation de ce
système (un modèle (W,R,r)), le programme satisfait-il la
spécification ? En termes logiques :
(W,R,r) est-il un modèle de F ?
Ce problème est appelé vérification de modèle
(``model-checking'' en anglais).
4.1 Machines séquentielles et vérification de modèle

Figure 1: Une machine séquentielle
L'exemple typique de vérification de modèle vient du domaine de la
vérification de matériel. Les réalisations, ou circuits, sont
décrits comme des machines séquentielles ayant m bits
d'entrée, n bits de sortie, et p bits d'état interne. Les
machines séquentielles fonctionnent au rythme d'une horloge externe,
et à chaque tic de l'horloge, la relation de transition d de
la machine est calculée, prenant en argument l'entrée courante et
l'état interne courant, pour fournir la sortie et l'état interne
suivants, comme illustré en figure 1. La relation
de transition d peut envoyer chaque combinaison entrée/état
courant vers plusieurs combinaisons sortie/état suivant, ce qui
signifie que la machine peut être non déterministe.
Formellement, la relation de transition est une relation d de
Bm+p vers Bn+p. Une machine séquentielle
définit un cadre de Kripke dont les mondes sont les (m+n+p)-uplets
de booléens, ou bits, représentant l'entrée, la sortie et
l'état courant, et dont la relation d'accessibilité R est
donnée par (i1, ..., im, s1, ..., sp, o'1, ...,
o'n) R (i'1, ..., i'm, s'1, ..., s'p, o1,
..., on) si et seulement si (i1, ..., im, s1, ...,
sp) d (s'1, ..., s'p, o1, ..., on).
Nous décrivons maintenant la technique de vérification
symbolique de modèle (``symbolic model-checking''). Cette
technique, utilisée avec des BDD, a rencontré un franc succès en
vérification de matériel. Pour plus de détails, voir
[McM93]. Nous donnons l'exemple de la
vérification symbolique de modèle de formules du µ-calcul
modal avec une seule modalité (que nous écrirons  , comme en
S4, mais signifiant ``à tout état immédiatement successeur'')
par rapport aux machines séquentielles.
, comme en
S4, mais signifiant ``à tout état immédiatement successeur'')
par rapport aux machines séquentielles.
Remarquer que le cadre de Kripke est proprement gigantesque : il a
2m+n+p états, et donc il est impossible de le représenter
sous forme de graphe en mémoire même pour de petites valeurs de
m, n, et p. Mais nous pouvons le représenter par une formule
propositionnelle, que nous noterons encore d, construire à
l'aide de m+n+2p variables i1, ..., im, s1,
..., sp, s'1, ..., s'p, o1, ...,
on. La taille de cette formule est grosso modo proportionnelle
au nombre de portes dans le circuit codant la machine séquentielle,
et est donc beaucoup plus acceptable.
Les variables s1, ..., sp sont appelées variables d'état. Un état de la machine séquentielle est
identifié à une affectation des variables d'état, d'entrée et
de sortie. Toute formule propositionnelle, et même toute formule
propositionnelle quantifiée sur l'ensemble des variables d'entrée,
d'état et de sortie dénote un ensemble de configurations
entrée/état/sortie (ou mondes) : l'ensemble des affectations qui
satisfont la formule. Par exemple, si A et B sont deux variables
d'état, alors AÚ B représente l'ensemble des états dans
lesquels A est vraie ou bien B est vraie.
L'idée fondamentale de la vérification symbolique de modèle
est : étant donné un cadre de Kripke représenté comme une
formule propositionnelle d portant sur les variables
d'entrée, d'état courant, d'état suivant et de sortie, et
étant donnée une formule modale F à vérifier sur le cadre
précédent, on calcule une formule propositionnelle (non modale)
Y portant sur les variables d'entrée, d'état et de sortie qui
représente l'ensemble des mondes où la formule modale F est
vraie. Alors, F est valide dans ce cadre de Kripke si et
seulement si Y est valide.
Nous devons récapituler et introduire quelques notions sur les
formules propositionnelles (non modales). Si F est une formule
propositionnelle, et A est une variable propositionnelle, "
A· F est la formule F[T/A] Ù F[F/A], et $
A· F est la formule F[T/A] Ú F[F/A]. Observons
aussi que :
Lemme 12
Soit F une formule propositionnelle, et A a variable
propositionnelle, telles que AÞ A' implique FÞ
F[A'/A]. (Nous disons que F est monotone en A.)
Alors il existe une formule propositionnelle µ A· F
(resp. n A· F) telle que :
- µ A· F est logiquement équivalent à F[(µ
A·F)/ A] (resp. n A· F est logiquement
équivalent à F[(n A·F)/ A]),
- et pour toute F' telle que F' est logiquement
équivalente à F [F'/A], alors µ A· F
implique F' (resp. F' implique n A· F).
Preuve : Soit A l'ensemble des affectations portant sur les variables
libres dans F.
Soit f l'application de P(A) vers P(A)
définie comme suit : si S est l'ensemble des affectations
satisfaisant une formule F', alors f(S) est l'ensemble des
affectations satisfaisant F[F'/A]. C'est bien une
application (le domaine de f est bien P(A)), car
tout S peut être décrit comme l'ensemble des affectations
satisfaisant une certaine formule F' construite sur A:
soit F' la disjonction de tous les A1rÙ A2r Ù ... Ù Anr, où r varie dans S, A
= {A1, ..., An} et Ar vaut A si r(A) est vrai
et ¬ A sinon.
Comme F est monotone par rapport à A, f est une fonction
croissante de P(A) vers P(A). Par le
théorème du point fixe de Knaster et Tarski, f a un plus petit
point fixe S et un plus grand point fixe
 . (Ce théorème dit que l'ensemble des points
fixes d'une application croissante d'un treillis complet, par
exemple P(A), dans lui-même en est un sous-treillis
non vide.) Soit µ A· F n'importe quelle formule
satisfaite exactement par les affectations de S, et
n A· F n'importe quelle formule satisfaite exactement par
les affectations de
. (Ce théorème dit que l'ensemble des points
fixes d'une application croissante d'un treillis complet, par
exemple P(A), dans lui-même en est un sous-treillis
non vide.) Soit µ A· F n'importe quelle formule
satisfaite exactement par les affectations de S, et
n A· F n'importe quelle formule satisfaite exactement par
les affectations de 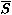 .
¤
.
¤
La preuve du lemme donne un moyen de calculer les plus petits et plus
grands points fixes de fonctions propositionnelles monotones. Dans le
cas de treillis finis (et P(A) est bien fini), la preuve
du théorème de Knaster et Tarski est constructive. Le plus petit
point fixe de f est obtenu comme l'union de f(Ø),
f(f(Ø)), ..., f(... f(Ø)...) (avec f
répété k fois), ..., cette suite devenant stationnaire au
plus tard pour k³ 2n, où n est le nombre de variables libres
de F. De même, le plus grand point fixe de f est obtenu
comme l'intersection de f(A), f(f(A)), ...,
f(... f(A)...) (avec f répété k fois),
..., cette suite étant stationnaire au plus tard pour k³
2n. Traduisons cette construction dans le langage des formules;
nous pouvons donc calculer µ A·F comme suit :
- Initialiser F' à F;
- calculer F'' = F' Ú F[F'/A];
- si F'' est logiquement équivalent à F', alors
retourner F';
- sinon, soit F' égale F'', et revenir à l'étape
2.
et de même, nous pouvons calculer n A·F comme suit :
- Initialiser F' à T;
- calculer F'' = F' Ù F[F'/A];
- si F'' est logiquement équivalente à F', alors
retourner F';
- sinon, soit F' égale F'', et revenir à l'étape
2.
L'essentiel de la vérification symbolique de modèle est alors,
comme McMillan en fait la remarque :
Théorème 13
Soit (W,d) un cadre de Kripke, où les mondes sont des
affectations portant sur les variables d'entrée ik, 1£
k£ m, les variables d'état sk, 1£ k£ p, et les
variables de sortie ok, 1£ k£ n; et où la relation
de transition est codée comme une formule propositionnelle
d sur ik, sk, ok et les variables
d'état suivant s'k, 1£ k£ p.
Soit [F] l'ensemble des affectations satisfaisant une
formule propositionnelle quantifiée F. Pour toute formule
propositionnelle F portant sur ik, sk et
ok uniquement, et pour tout monde w, w |= F est
caractérisé comme suit :
- w|= A si et seulement si wÎ[A], pour A
une des variables ik, sk ou ok;
- w|=FÚF' si et seulement si
wÎ[FÚF'] (et de même pour Ù, ¬,
Þ);
- w|=
 F si et seulement si wÎ["
s'1· ..." s'p· dÞ
F[s'1/s1,...,s'p/sp]];
F si et seulement si wÎ["
s'1· ..." s'p· dÞ
F[s'1/s1,...,s'p/sp]];
- w|=µ A·F si et seulement si wÎ[µ
A·F];
- w|=n A·F si et seulement si wÎ[n
A·F];
où dans les deux derniers cas, nous avons supposé que F
était monotone en A.
Le théorème fournit la traduction souhaitée des formules modales
F vers les formules propositionnelles non modales Y telle
que les configurations de (W,d) où F est vraie sont
représentées exactement par les affectations satisfaisant Y.
L'algorithme de traduction fonctionne comme suit :
- si F est une variable A, retourner A;
- si F=F'ÚF'', soit Y' la traduction de F'
et Y'' la traduction de F'', alors retourner Y' Ú
Y''; (de même pour Ù, ¬, Þ;)
- si F=
 F', soit Y' la traduction de F', et
retourner " s'1· ..." s'p·
dÞ Y'[s'1/s1,...,s'p/sp];
F', soit Y' la traduction de F', et
retourner " s'1· ..." s'p·
dÞ Y'[s'1/s1,...,s'p/sp];
- si F=µ A·F', soit Y' la traduction de
F', et retourner µ A·Y';
- si F=n A·F', soit Y' la traduction de
F', et retourner n A·Y'.
Que l'algorithme est correct est facile à montrer, sauf deux points
liés aux formules en µ et n. D'abord, la variable A n'est
une variable ni d'entrée, ni d'état, ni de sortie, ce qui, à
strictement parler, nous empêche d'utiliser le
théorème 13. Nous corrigeons ce problème en
ajoutant A à l'ensemble des variables d'entrée par exemple : on
vérifiera que d ne change pas. Ensuite, il n'est pas clair
que les traductions des opérateurs µ et n soient bien
définies, parce que nous devons d'abord nous assurer que la formule
Y' est monotone en A. La raison en est le lemme facile qui
suit :
Lemme 14 Soit F' une formule modale, où A n'apparaît que
positivement. Soit Y' la traduction de F'. Alors Y'
est monotone en A.
4.2 Diagrammes de décision binaire
Pour savoir si la formule modale F est valide dans le cadre de
Kripke donné, il est nécessaire et suffisant de vérifier que la
formule traduite Y est valide.
Cependant, le calcul des points fixes µ A·Y et n
A·Y est ardu, parce que nous devons faire un test
d'équivalence logique à chaque passage de la boucle. Remarquer
que la vérifier de l'équivalence de deux formules Y1 et
Y2 revient à vérifier la validité de
Y1ÛY2, et ceci peut prendre un temps exponentiel en
les tailles de Y1 et Y2.
Nous pouvons économiser une grande partie de ce coût dans les
applications pratiques si nous représentons les formules
propositionnelles sous une forme canonique sur laquelle les
opérations propositionnelles sont efficaces. Les diagrammes de
décision binaire (BDD) ont toutes les propriétés souhaitées.
En particulier, la négation s'effectue en temps linéaire (même
constant si on utilise des TDG, un raffinement des BDD), et toutes les
opérations binaires opèrent en temps proportionnel à smn, où
m et n sont les tailles des BDD à combiner, et s est le coût
du partage.
Pour utiliser les BDD efficacement, cependant, il nous faut encore
définir la notion de substitution sur les BDD. Sur les formules
construites à l'aide de Ú, Ù, ¬, Þ, la
substitution était juste le remplacement textuel. Mais si F
est un BDD, nous voulons que F [F'/A] soit le BDD de la
formule Y [F'/A], où Y est n'importe quelle formule
représentée par le BDD F. Ceci n'est pas un simple
remplacement textuel, qui ne fournit pas un BDD en général.
Nous définissons d'abord F[T/A] et F[F/A] par
récurrence structurelle sur F:
- T[T/A]=T, F[T/A]=F, T[F/A]=T, F[F/A]=F;
- si F=A¾®F+;F-, alors
F[T/A]=F+, F[F/A]=F-;
- si F est de la forme
A'¾®F+:F-, avec A'¹ A,
alors
F[T/A]= BDDmake(A', F+[T/A],
F-[T/A]), et F[F/A]= BDDmake(A',
F+[F/A], F-[F/A]).
Nous pouvons alors calculer F[F'/A] comme (F'ÞF[T/A])Ù
(¬F'ÞF[F/A]), ou comme (F'ÙF[T/A])Ú
(¬F'ÙF[F/A]).
C'est tout ce dont nous avons besoin pour calculer des quantifications
propositionnelles et des points fixes : nous avons tous les outils
nécessaires à la vérification symbolique de modèle à l'aide
de BDD.
4.3 Développements
Le codage de la relation de transition d comme une formule
propositionnelle entre m variables d'entrée, 2p variables
d'état courant et suivant, et n variables de sortie n'est pas
économique. En particuler, si le circuit est déterministe, d est en fait une fonction de
Bm+p (entrée et état courant) vers Bp+n (état
suivant et sortie). Alors on peut représenter d comme un
(p+n)-uplet de fonctions d1, ..., dp+n de
Bm+p vers B, autrement dit comme un (p+n)-uplet de
formules sur m+p variables. Ceci est très important, car la
taille d'un BDD sur k variables peut atteindre une taille de l'ordre
de 2k. (Plus précisément, la borne supérieure est 2k/k.)
Par exemple, dans le cas m=n=0, le BDD pour d sur les 2p
variables d'état courant et suivant peut avoir une taille
proportionnelle au carré de la plus grande taille des BDD de
di, 1£ i£ p+n : en pratique, la représentation
sous forme de (p+n)-uplets permet de vérifier des circuits en
quelques mégaoctets de mémoire qui nécessiteraient plus
gigaoctets ou téraoctets dans la représentation précédente.
(Ceci sans parler du temps qu'il nous faudrait pour construire de
telles structures en mémoire.)
Si le circuit est non déterministe, nous pouvons encore utiliser une
variante de la représentation sous forme de (p+n)-uplet. Nous
pouvons en général décrire le degré de non-déterminisme en
quelques bits seulement : c'est-à-dire, nous savons qu'il n'y aura
jamais plus de, disons, 2k mondes en relation avec un monde donné
quelconque, où k est usuellement petit (au moins comparé à
p). Nous créons alors k variables propositionnelles auxiliaires
x1, ..., xk, et codons d comme l'union de 2k
fonctions paramétrées dr, où r est une
affectation de valeurs de vérité à xi, 1£ i£ k.
La vérification de modèle se pratique comme avant, sauf que le
troisième cas du théorème 13 doit devenir :
- si F=
 F', soit Y' la traduction de F',
F', soit Y' la traduction de F',
et retourner " x1· ..." xk·
Y'[d1(i1, ..., im, s1, ...,
sp)/s1, ..., dp(i1, ..., im, s1,
..., sp)/sp];
Remarquer que dans le cas déterministe, nous n'avons même plus
besoin de quantification.
Une autre variante de la méthode de base porte sur la façon dont
nous représentons les ensembles de configurations. Nous avons
utilisé des formules F représentant des ensembles de
configurations comme l'ensembles des affectations qui les satisfont.
C'est-à-dire, si l'on considère F comme une application de
Bm+p+n vers B, que nous représentons des ensembles de
configurations comme l'image inverse F-1({T}). Une
façon de faire duale est de prendre un (m+p+n)-uplet
d'applications booléennes Fi, 1£ i£ m+p+n, de
Bm+p vers B, et de représenter des ensembles de
configurations comme l'image directe de Bm+p par ce
(m+p+n)-uplet
Finalement, nous devons mentionner que vérifier qu'une formule
modale F est toujours vraie (dans tous les mondes) n'est pas en
général ce que nous voulons. Une machine séquentielle démarre
en effet dans une configuration donnée (disons, toutes les entrées
et tous les bits d'état mis à F), et alors elle ne passe que
par les configurations atteignables depuis cette configuration
initiale. Par exemple, un compteur à 2 bits censé compter 0,
1, 2, 0, 1, 2, etc. (correspondant aux configurations
(F,F), (F,T), (T,F) respectivement) n'atteindra jamais la
configuration où les deux bits sont T. Ce que nous voulons en
fait, c'est vérifier que la formule modale F est vraie dans
tous les états atteignables, pas nécessairement dans tous les
mondes.
Une façon naïve de le faire est de calculer la traduction non
modale Y de F par rapport au cadre de Kripke donné comme
avant, ensuite de calculer une formule Y' telle que les
affectations qui la satisfont sont exactement les configurations
atteignables, et alors de vérifier que Y'ÞY est valide.
Ceci est cependant trop coûteux en pratique, et il est intéressant
d'élaguer le BDD Y en utilisant l'ensemble des configurations
atteignables lors de sa construction.
On trouvera des discussions plus poussées de la vérification de
modèle à l'aide de BDD et des applications dans
[McM93]. [CM95] est une bonne
source de références bibliographiques. Un traitement plus en
profondeur des logiques modales et temporelles en informatique se
trouve dans [Sti92, Eme90]. Les logiques
modales sont le sujet de [GG84].








 , comme en
S4, mais signifiant ``à tout état immédiatement successeur'')
par rapport aux machines séquentielles.
, comme en
S4, mais signifiant ``à tout état immédiatement successeur'')
par rapport aux machines séquentielles. . (Ce théorème dit que l'ensemble des points
fixes d'une application croissante d'un treillis complet, par
exemple P(A), dans lui-même en est un sous-treillis
non vide.) Soit µ A· F n'importe quelle formule
satisfaite exactement par les affectations de S, et
n A· F n'importe quelle formule satisfaite exactement par
les affectations de
. (Ce théorème dit que l'ensemble des points
fixes d'une application croissante d'un treillis complet, par
exemple P(A), dans lui-même en est un sous-treillis
non vide.) Soit µ A· F n'importe quelle formule
satisfaite exactement par les affectations de S, et
n A· F n'importe quelle formule satisfaite exactement par
les affectations de 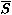 .
¤
.
¤ F si et seulement si wÎ["
s'1· ..." s'p· dÞ
F[s'1/s1,...,s'p/sp]];
F si et seulement si wÎ["
s'1· ..." s'p· dÞ
F[s'1/s1,...,s'p/sp]];
 F', soit Y' la traduction de F', et
retourner " s'1· ..." s'p·
dÞ Y'[s'1/s1,...,s'p/sp];
F', soit Y' la traduction de F', et
retourner " s'1· ..." s'p·
dÞ Y'[s'1/s1,...,s'p/sp];
 F', soit Y' la traduction de F',
F', soit Y' la traduction de F',

