


3 Autres logiques modales utilisées en informatique
Un échantillon de logiques modales utilisées encore plus
couramment en informatique consiste en la logique de Hennessy-Milner
ou HML, qui a été inventée pour fournir un langage logique de
description des processus parallèles du langage CCS de Milner; en
des logiques temporelles comme CTL, conçues pour fournir un
langage plus riche de spécification de circuits matériels, ou la
logique propositionnelle dynamique (PDL), qui est essentiellement la
logique de Hoare (une logique servant à raisonner sur des
programmes), présentée de façon plus succincte et plus
élégante. Nous nous intéresserons principalement au
µ-calcul modal de Kozen, une logique plus générale que celles
mentionnées ci-dessus. (Voir [Mil89] pour CCS et HML,
[Eme90] pour les logiques temporelles, et
[KT90] pour la logique dynamique.)
L'idée de départ dans ces logiques est qu'elles fournissent un
langage suffisamment riche pour exprimer des propriétés utiles sur
des automates (à savoir des machines à états finis, encore
connues sous le nom de graphes états-transitions étiquetés). Un
automate est un ensemble S d'états, muni d'une relation de
transition R entre les états. (Nous laissons de côté les
états initiaux et finaux dans cette définition.) Une transition est un couple (s,s') d'états dans R, et on la
suppose étiquetée par une lettre prise dans un alphabet fini A. Nous notons s 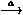 s' la transition (s,s') étiquetée
par a. Alors nous pouvons considérer S4 ou des logiques
temporelles plus compliquées comme des langages d'expression de
propriétés sur des automates, vus comme des cadres de Kripke : par
exemple, en S4, le fait que
s' la transition (s,s') étiquetée
par a. Alors nous pouvons considérer S4 ou des logiques
temporelles plus compliquées comme des langages d'expression de
propriétés sur des automates, vus comme des cadres de Kripke : par
exemple, en S4, le fait que  F soit satisfaite à l'état
s signifierait que F est satisfiate à tous les états que
nous pouvons atteindre depuis s en suivant un nombre fini de
transitions. (Les chemins que nous pouvons prendre représentent tous
les futurs possibles de s.)
F soit satisfaite à l'état
s signifierait que F est satisfiate à tous les états que
nous pouvons atteindre depuis s en suivant un nombre fini de
transitions. (Les chemins que nous pouvons prendre représentent tous
les futurs possibles de s.)
La logique de Hennessy-Milner logic (HML) est une version à
plusieurs agents de la logique modale de base K; au lieu de n'avoir
qu'une seule modalité  (resp. à), nous avons
plusieurs modalités [s] (resp. á sñ), correspondant
chacune à un ensemble possible s de transitions dans un automate
représentant toutes les exécutions possibles d'un programme CCS.
Les transitions dans ces systèmes sont censées représenter des
actions atomiques individuelles, comme envoyer ou recevoir un message.
Les transitions peuvent être composées en séquence ou en
parallèle. De plus, les transitions peuvent se synchroniser, et
c'est la façon dont des processus tournant en parallèle arrivent
à communiquer : pour chaque transition i (par exemple, ``envoyer
tel message''), il existe une transition correspondante distincte
(resp. à), nous avons
plusieurs modalités [s] (resp. á sñ), correspondant
chacune à un ensemble possible s de transitions dans un automate
représentant toutes les exécutions possibles d'un programme CCS.
Les transitions dans ces systèmes sont censées représenter des
actions atomiques individuelles, comme envoyer ou recevoir un message.
Les transitions peuvent être composées en séquence ou en
parallèle. De plus, les transitions peuvent se synchroniser, et
c'est la façon dont des processus tournant en parallèle arrivent
à communiquer : pour chaque transition i (par exemple, ``envoyer
tel message''), il existe une transition correspondante distincte
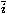 (``recevoir tel message''), telle que de deux processus
dont l'un est prêt à déclencher i et l'autre
(``recevoir tel message''), telle que de deux processus
dont l'un est prêt à déclencher i et l'autre 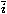 ,
peuvent déclencher les deux en même temps et continuer
l'exécution. L'exécution procède en déclenchant les
transitions d'un état au suivant. Un état est souvent appelé un
agent ou un processus. Nous écrivons A
,
peuvent déclencher les deux en même temps et continuer
l'exécution. L'exécution procède en déclenchant les
transitions d'un état au suivant. Un état est souvent appelé un
agent ou un processus. Nous écrivons A 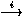 A' pour dire que l'agent A peut se transformer en l'agent A' en
suivant la transition i.
A' pour dire que l'agent A peut se transformer en l'agent A' en
suivant la transition i.
La logique de Hennessy-Milner représente les comportements des
processus par des formules modales. Le fait qu'un agent A
satisfasse [s]F, où s est un ensemble de transitions,
signifie : ``pour toute transition A  A' avec iÎ s,
A' satisfait F'', et á sñF (i.e.,
¬[s]¬F) signifie : ``il y a une transition A
A' avec iÎ s,
A' satisfait F'', et á sñF (i.e.,
¬[s]¬F) signifie : ``il y a une transition A 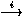 A' avec iÎ s telle que A' satisfait F''. Bien que ce ne
soit pas nécessaire, nous nous restreignons maintenant à des
ensembles finis de transitions, par souci de simplicité.
A' avec iÎ s telle que A' satisfait F''. Bien que ce ne
soit pas nécessaire, nous nous restreignons maintenant à des
ensembles finis de transitions, par souci de simplicité.
D'après les définitions, nous pouvons supposer que
[{i1,...,in}]F est une abréviation de
[i1]FÙ...Ù[in]F (ou d'une formule valide
quelconque T si n=0), où [i]F signifie [{i}]F.
Alors les axiomes sont ceux de la logique propositionnelle classique
plus :
- (K) [i](AÞ B)Þ [i]AÞ [i]B,
avec une règle de nécessitation modifiée :
- (Nec) de F, déduire [i]F, pour toute formule F
et toute transition i.
Cette logique peut être rendue plus expressive en l'étendant par,
par exemple, un opérateur de plus petit point fixe µ et un
opérateur de plus grand point fixe n; nous obtenons le µ-calcul modal.
L'idée est que, si A est une variable propositionnelle qui
n'apparaît que positivement dans F (en supposant que Þ
a été remplacé par ¬ et Ú, ceci signifie que A est
à l'intérieur d'un nombre pair de négations; c'est un critère
syntaxique assurant que si AÞ A' est vrai, alors
FÞF[A'/A] est vrai aussi), alors µ A·F et n
A·F sont deux formules F' logiquement équivalentes à
F[F'/A] : ce sont des points fixes de la fonction A
|® F, modulo l'équivalence logique. De plus, chaque fois
que F' est une formule telle que F' est équivalente à
F[F'/A], alors µ A·FÞ F' et F'Þn
A·F sont vraies. On a donc les axiomes et règles
suivants :

Intuitivement, µ A·F est le plus petit point fixe de la
fonction f qui à A associe F, c'est-à-dire la disjonction
de toutes les formules f(f(... f(F)...)), où il y a n
occurrences de f, nÎN, et où F est une formule donnée
représentant le faux. Réciproquement, n A·F est
intuitivement la conjonction de toutes les formules f(f(...
f(T)...)), où il y a n occurrences de f, nÎN, et
où T est une formule représentant le vrai.
Les opérateurs µ et n nous permettent d'exprimer des
propriétés qui ne pouvaient pas être décrites en HML, parce
que µ et n incorporent une forme de récurrence que nous
n'avions pas en HML. Par exemple, la vivacité (``liveness'' en
anglais) peut s'exprimer n A·á AñTÙ[A] A, où A est l'ensemble de
toutes les lettres de transitions; ceci veut dire qu'à chaque
étape de calcul, nous pouvons exécuter une transition, et quelle
que soit la transition que nous choisissions, nous pouvons alors
encore exécuter une transition, et ainsi de suite. Nous pouvons
aussi écrire qu'un processus peut bloquer (``deadlock'' en anglais)
comme µ A·[A]FÚá Añ A. En
général, si F ne dépend pas de A, µ
A·FÚá Añ A exprime qu'il existe un
chemin d'exécution tel que F finit par être satisfait sur ce
chemin, alors que µ A·FÚ[A]A dit que, sur tous
les chemins d'exécution, F finit par être satisfait
(autrement dit, F est inévitable). Une formule plus
compliquée comme n B·(µ A·FÚ[A]A)Ù
á AñTÙ [A] B dit que F est vraie
infiniment souvent sur chaque chemin d'exécution. (La µ-formule
interne signifie que F finit par être vraie, donc la formule
tout entière dit que F finit par être vraie en un état, et
qu'alors nous pouvons suivre une transition, et quelle que soit celle
que nous choisissions, F finira par redevenir vraie, et ainsi de
suite.)
Parce qu'il incorpore une forme de récurrence, le µ-calcul modal
n'est pas compact (contrairement à la logique propositionnelle par
exemple) :
Théorème 10 [Non-compacité] Il existe un ensemble infini G de formules du µ-calcul
modal, et une formule du µ-calcul modal F, tels que G
|= F et qu'il est faux que D |= F pour aucun
sous-ensemble fini D de G.
Preuve : Soit G l'ensemble contenant µ B · A Ú á
añ B (qui dit qu'il existe un monde accessible depuis le
monde courant par un nombre fini de transitions a et où A est
vrai), et ¬ A, ¬á añ A, ¬á
añá añ A, ..., et soit F n'importe quelle
formule insatisfiable.
On a G|=F, parce que G n'est satisfaite dans
aucun modèle.
Cependant, pour tout sous-ensemble fini D de G, on
peut construire un modèle de D comme suit : soit k un
entier tel que pour tout j³ k, ¬á
añ...á añ A (avec j fois la modalité
á añ) n'est pas dans D, et on construit le
graphe orienté consistant en exactement un circuit de k+1
états, numérotés de 0 à k; on définit Ra comme la
relation qui envoie chaque sommet du circuit vers son successeur
(autrement dit, i vers i+1 si 0£ i<k, et k vers 0), et
soit r une affectation rendant A vrai à l'état k
uniquement. À l'état 0, µ B · A Ú á añ
B est vraie, et pour tout j<k, ¬ á
añ...á añ A (avec j fois á a
ñ) est vrai aussi, puisque A n'est pas vrai à l'état
j. Donc il s'agit d'un modèle de D, mais ce n'est pas un
modèle de F (car F n'a pas de modèle), et donc non
D|=F.
¤
Mais le µ-calcul modal reste décidable :
Théorème 11 [Decidabilité] Le problème de la satisfiabilité des formules du µ-calcul
modal est décidable.
Le problème est en fait DEXPTIME-complet, mais c'est très
difficile à montrer : les filtrations ne fonctionnent plus (bien que
la propriété de petit modèle soit toujours vraie) et aucune
axiomatisation finie complète n'est connue pour cette logique
[KT90].






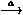 s' la transition (s,s') étiquetée
par a. Alors nous pouvons considérer S4 ou des logiques
temporelles plus compliquées comme des langages d'expression de
propriétés sur des automates, vus comme des cadres de Kripke : par
exemple, en S4, le fait que
s' la transition (s,s') étiquetée
par a. Alors nous pouvons considérer S4 ou des logiques
temporelles plus compliquées comme des langages d'expression de
propriétés sur des automates, vus comme des cadres de Kripke : par
exemple, en S4, le fait que  F soit satisfaite à l'état
s signifierait que F est satisfiate à tous les états que
nous pouvons atteindre depuis s en suivant un nombre fini de
transitions. (Les chemins que nous pouvons prendre représentent tous
les futurs possibles de s.)
F soit satisfaite à l'état
s signifierait que F est satisfiate à tous les états que
nous pouvons atteindre depuis s en suivant un nombre fini de
transitions. (Les chemins que nous pouvons prendre représentent tous
les futurs possibles de s.) (resp. à), nous avons
plusieurs modalités [s] (resp. á sñ), correspondant
chacune à un ensemble possible s de transitions dans un automate
représentant toutes les exécutions possibles d'un programme CCS.
Les transitions dans ces systèmes sont censées représenter des
actions atomiques individuelles, comme envoyer ou recevoir un message.
Les transitions peuvent être composées en séquence ou en
parallèle. De plus, les transitions peuvent se synchroniser, et
c'est la façon dont des processus tournant en parallèle arrivent
à communiquer : pour chaque transition i (par exemple, ``envoyer
tel message''), il existe une transition correspondante distincte
(resp. à), nous avons
plusieurs modalités [s] (resp. á sñ), correspondant
chacune à un ensemble possible s de transitions dans un automate
représentant toutes les exécutions possibles d'un programme CCS.
Les transitions dans ces systèmes sont censées représenter des
actions atomiques individuelles, comme envoyer ou recevoir un message.
Les transitions peuvent être composées en séquence ou en
parallèle. De plus, les transitions peuvent se synchroniser, et
c'est la façon dont des processus tournant en parallèle arrivent
à communiquer : pour chaque transition i (par exemple, ``envoyer
tel message''), il existe une transition correspondante distincte
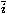 (``recevoir tel message''), telle que de deux processus
dont l'un est prêt à déclencher i et l'autre
(``recevoir tel message''), telle que de deux processus
dont l'un est prêt à déclencher i et l'autre 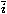 ,
peuvent déclencher les deux en même temps et continuer
l'exécution. L'exécution procède en déclenchant les
transitions d'un état au suivant. Un état est souvent appelé un
agent ou un processus. Nous écrivons A
,
peuvent déclencher les deux en même temps et continuer
l'exécution. L'exécution procède en déclenchant les
transitions d'un état au suivant. Un état est souvent appelé un
agent ou un processus. Nous écrivons A 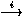 A' pour dire que l'agent A peut se transformer en l'agent A' en
suivant la transition i.
A' pour dire que l'agent A peut se transformer en l'agent A' en
suivant la transition i. A' avec iÎ s,
A' satisfait F'', et á sñF (i.e.,
¬[s]¬F) signifie : ``il y a une transition A
A' avec iÎ s,
A' satisfait F'', et á sñF (i.e.,
¬[s]¬F) signifie : ``il y a une transition A 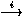 A' avec iÎ s telle que A' satisfait F''. Bien que ce ne
soit pas nécessaire, nous nous restreignons maintenant à des
ensembles finis de transitions, par souci de simplicité.
A' avec iÎ s telle que A' satisfait F''. Bien que ce ne
soit pas nécessaire, nous nous restreignons maintenant à des
ensembles finis de transitions, par souci de simplicité.


