


2 S4 et logiques non monotones
2.1 Syntaxe
Les formules de S4 sont toutes les formules construites à partir de
variables propositionnelles à l'aide des connecteurs propositionnels
usuels Ù, Ú, ¬, Þ, et la modalité
 : si F est une formule, alors
: si F est une formule, alors  F est une formule
aussi (``box F'', ou ``nécessairement, F''; en termes
temporels, ``dans tout futur, F''). Nous supposons que
F est une formule
aussi (``box F'', ou ``nécessairement, F''; en termes
temporels, ``dans tout futur, F''). Nous supposons que  a
une priorité plus forte que tous les autres opérateurs logiques,
de sorte que
a
une priorité plus forte que tous les autres opérateurs logiques,
de sorte que  AÞ A est une abréviation de (
AÞ A est une abréviation de ( A)Þ
A, par exemple. Nous définissons aussi à F comme une
abréviation de ¬
A)Þ
A, par exemple. Nous définissons aussi à F comme une
abréviation de ¬ ¬ F (``possiblement, A''; en termes
temporels, ``à un moment dans un futur, A'').
¬ F (``possiblement, A''; en termes
temporels, ``à un moment dans un futur, A'').
En plus des règles de preuve de la logique classique, en S4 nous
ajoutons les axiomes suivants :
- (K)
 (FÞ F')Þ
(FÞ F')Þ FÞ
FÞ F'
F'
- (T)
 FÞ F
FÞ F
- (4)
 FÞ
FÞ 
 F
F
pour toutes formules F et F', et en plus de la règle de
modus ponens (MP) rule, nous avons la règle de nécessitation :
- (Nec) de F, déduire
 F, pour chaque formule F.
F, pour chaque formule F.
Les axiomes (K) et (T) sont communs à la plupart des logiques
modales. L'axiome (K) dit que si FÞF' et F sont
nécessaires (ou vraies dans tout futur), alors F' est
nécessaire (ou vraie dans tout futur, dans l'interprétation
temporelle). L'axiome (T) et la règle (Nec) ont été
commentées au début de ce chapitre.
L'ensemble des axiomes (K) et (T) est aussi appelé (S). La logique
S4 est en fait nommée d'après ses axiomes, et est aussi parfois
appelée KT4.
Ce qui fait de S4 une logique particulière est principalement
l'axiome (4). Dans l'interprétation de  comme un opérateur
de futur, (4) exprime la transitivité du temps, c'est-à-dire que
si F est vraie dans tous les futurs, alors elle est aussi vraie
dans tous les futurs de tous ces futurs.
comme un opérateur
de futur, (4) exprime la transitivité du temps, c'est-à-dire que
si F est vraie dans tous les futurs, alors elle est aussi vraie
dans tous les futurs de tous ces futurs.
Comme nous l'avons remarqué précédemment, les systèmes de
Hilbert ne sont pas faciles à manipuler, et nous allons voir la
sémantique de S4 en section 2.3, et des systèmes
de séquents en section 2.5.
2.2 Logique philosophique et logiques non monotones
Il existe une multitude d'autres logiques modales venant de la
communauté de logique philosophique. Toutes ont la règle (Nec);
la plupart sont fondées sur l'axiome (K), et sont alors appelées
logiques modales normales. Certaines utilisent l'axiome (T).
D'autres axiomes utilisés pour définir des logiques modales sont :
- (5) àFÞ
 àF,
àF,
- (D)
 FÞàF,
FÞàF,
- (R) à
 FÞ(FÞ
FÞ(FÞ F),
F),
- (F) (
 FÞF')Ú(à
FÞF')Ú(à F'ÞF),
F'ÞF),
- (2) à
 FÞ
FÞ àF
àF
(T) est parfois nommé (M), (5) parfois (E) (pour ``euclidien''), et
(R) est parfois appelé (W5).
Nous n'examinerons pas ce que les diverses combinaisons de ces axiomes
signifient : voir le livre de Chellas.
Dans toute logique modale L, on peut définir une notion de
déduction |-L : si G est un ensemble de formules, et
F est une formule, G|-LF si et seulement si
F peut être déduite de l'ensemble d'hypothèses G et
des axiomes de L en utilisant uniquement les règles (MP) et (Nec).
Mais, comme nous l'avons déjà dit, le théorème de la
déduction n'est pas valide dans les logiques modales, autrement dit
F1, ..., Fn |-L F n'est pas équivalent à
|-L F1 Þ ... Þ Fn Þ F (bien que
ce dernier implique le premier).
Cette définition de la déductibilité est adaptée de celle de
Rajeev Goré [Gor91], et est appelée déductibilité forte. La déductibilité faible est
la relation |-L définie par G |-L F si
et seulement s'il existe un sous-ensemble fini {F1, ...,
Fn} de G tel que |-L F1 Þ ...
Þ FnÞ F. (Remarquer que, de façon paradoxale,
la déductibilité faible implique la déductibilité forte, mais
pas l'inverse.)
Les déductibilités faible et forte coïncident lorsque
l'ensemble d'hypothèses G est vide, et une formule F
telle que |-LF (autrement dit, |-LF) est
appelée un théorème de L.
Un des grands intérêts des logiques modales est que la
déductibilité forte plus un certain processus de complétion
forment l'essence des logiques non monotones, qu'elles soient
modales ou non. En traduisant Rajeev Goré [Gor91] :
Les logiques modales propositionnelles sont depuis quelque temps
utilisées pour modéliser des notions épistémiques comme la
connaissance et la croyance, où la formule  A se lit ``on
croit que A'' ou ``on sait A''. Étant donnée une logique
modale S (monotone) et un ensemble de formules G, la
formule A est une conséquence monotone de G dans S
si elle est déductible dans S à partir de G, ce que
l'on écrit usuellement G |-S A. L'ensemble G
est habituellement appelé une théorie et les conséquences
monotones de G dans S sont les formules déductibles
de G dans S; c'est-à-dire CnS(G) = {A|
G |-S A}. Le système est ``monotone'' en ce sens
que si A est dans CnS(G), alors elle sera dans
CnS(G') pour tout sur-ensemble G' de G.
A se lit ``on
croit que A'' ou ``on sait A''. Étant donnée une logique
modale S (monotone) et un ensemble de formules G, la
formule A est une conséquence monotone de G dans S
si elle est déductible dans S à partir de G, ce que
l'on écrit usuellement G |-S A. L'ensemble G
est habituellement appelé une théorie et les conséquences
monotones de G dans S sont les formules déductibles
de G dans S; c'est-à-dire CnS(G) = {A|
G |-S A}. Le système est ``monotone'' en ce sens
que si A est dans CnS(G), alors elle sera dans
CnS(G') pour tout sur-ensemble G' de G.
Pour obtenir la non-monotonie nous faisons l'hypothèse que
¬ A (``on ne sait pas A'') s'il n'y a pas de déduction
de A dans S à partir de G et des hypothèses
précédentes. Plus formellement, la théorie T est une S-expansion de la théorie G si elle satisfait
l'équation T = CnS(G È {¬
A (``on ne sait pas A'') s'il n'y a pas de déduction
de A dans S à partir de G et des hypothèses
précédentes. Plus formellement, la théorie T est une S-expansion de la théorie G si elle satisfait
l'équation T = CnS(G È {¬ A | A Ï T}). Comme T apparaît sur le côté droit, la
définition est circulaire, et conséquemment, une théorie
G peut avoir zéro, une ou plusieurs S-expansions.
Pour contre-balancer ce phénomène, l'ensemble des conséquences
non monotones de G dans S est usuellement
défini comme l'intersection de toutes les S-expansions de
G. Le nouveau système est ``non-monotone'' parce que, bien
que A puisse être une conséquence non monotone de G,
elle peut ne pas être une conséquence non monotone d'un
sur-ensemble de G.
A | A Ï T}). Comme T apparaît sur le côté droit, la
définition est circulaire, et conséquemment, une théorie
G peut avoir zéro, une ou plusieurs S-expansions.
Pour contre-balancer ce phénomène, l'ensemble des conséquences
non monotones de G dans S est usuellement
défini comme l'intersection de toutes les S-expansions de
G. Le nouveau système est ``non-monotone'' parce que, bien
que A puisse être une conséquence non monotone de G,
elle peut ne pas être une conséquence non monotone d'un
sur-ensemble de G.
L'intérêt porté aux logiques non monotones apparaît
lorsqu'on cherche à capturer la notion de raisonnement de tous les
jours, où des conclusions par défaut sont obtenues à partir
d'informations incomplètes, pour être éventuellement
rétractées lors de l'apparition de contre-exemples. La circonscription de John McCarthy a été la première
tentative de formalisation du raisonnement de tous les jours, suivie
par la logique des cas par défaut de Reiter (default
logic) et de la logique auto-épistémique de Halpern
et Moses. Marek, Schwarz et Truszczynski ont ensuite remarqué que
la logique auto-épistémique n'était rien d'autre que K45D non
monotone, et que S4F généralisait aussi bien la logique des cas
pas défaut que la logique auto-épistémique.
2.3 Sémantique de Kripke
La sémantique des logiques modales comme S4 sont usuellement
décrites au moyen d'interprétations en termes de mondes
possibles (possible worlds interpretations). En effet, une
formule n'est pas juste vraie dans une interprétation, mais aussi
dans un certain état, par exemple à un instant donné. Nous
représentons l'ensemble de tous les états (par exemple, de tous
les instants) par un univers W non vide, dont les points,
les états, sont appelés les mondes. Dans le cas de S4, les
mondes sont partiellement ordonnés : si w et w' sont des mondes
(des instants), w£ w' signifie que w est un instant qui est
avant w'. Alors une formule  F est vraie dans un monde w
si et seulement si F est vraie dans tous les mondes qui le
suivent (à tous les instants ultérieurs).
F est vraie dans un monde w
si et seulement si F est vraie dans tous les mondes qui le
suivent (à tous les instants ultérieurs).
La définition se généralise à toutes les logiques modales de
la façon suivante, due à Saul Kripke in 1963 :
Définition 1 Un cadre de Kripke (Kripke frame) est un couple
(W,R), où W est un ensemble non vide appelé l'univers et R est une relation binaire sur W appelée la
relation d'accessibilité. Les éléments de W sont
appelés les mondes.
Une affectation ou interprétation r est une
fonction des variables propositionnelles vers les ensembles de
mondes.
La sémantique d'une formule modale F est définie par la
fonction à valeurs booléennes [F] w r, où w est
un monde et r est une affectation. Nous notons w, r
|=F pour [F] w r = T, et définissons :
- w,r|= A si et seulement si wÎr(A), où A
est une variable propositionnelle;
- w,r|=FÙF' si et seulement si
w,r|=F et w,r|=F';
- w,r|=FÚF' si et seulement si
w,r|=F ou w,r|=F';
- w,r|=¬F si et seulement si non
w,r|=F;
- w,r|=FÞF' si et seulement si non w,r
|=F ou w,r|=F';
- w,r|=
 F si et seulement si pour tout monde
w' tel que w R w', alors w'|=F.
F si et seulement si pour tout monde
w' tel que w R w', alors w'|=F.
Lorsque w,r|=F, nous disons que w,r satisfait F.
Un cadre de Kripke est satisfait par F, ou est un modèle de F si et seulement si w, r |=F
pour un certain monde w et une certaine affectation r.
F est valide dans le cadre donné si et seulement si
w, r |= F pour tout monde w et toute affectation
r.
Si C est une classe de cadres, nous disons que F est
valide dans C, ce que nous notons C|=F, si et seulement si F est valide dans tout
cadre de la classe.
Remarquer que, si l'on regarde R comme un ensemble de couples, un
cadre de Kripke (W,R) n'est rien d'autre qu'un graphe
orienté de sommets les éléments de W et d'arcs les
éléments de R.
Il s'avère qu'une formule de S4 est un théorème si et seulement
si elle est valide dans la classe des ensembles pré-ordonnés,
c'est-à-dire des cadres (W,R) tels que R est une relation
réflexive et transitive sur W. Si l'on voit les cadres comme des
graphes, ceci signifie que les théorèmes de S4 sont en fait des
théorèmes portant sur l'ensemble des chemins dans les collections
de graphes orientés acycliques (en fait, les arbres suffisent).
Plus précisément :
Définition 2 Soit C une classe de cadres, et L une logique modale.
L est correcte pour C si et seulement si pour toute
formule F, |-LF implique C |=F.
L est complète par rapport à C si et seulement
si pour toute formule F, C |=F implique
|-LF.
On caractérise les cadres par les propriétés de leur relation
d'accessibilité R : elles peuvent être réflexives,
symétriques, transitives, séquentielles (``serial'' en anglais :
depuis chaque monde il existe un monde accessible), convergentes (pour
tout monde w, si w1 et w2 sont accessibles depuis w,
alors il y a un monde accessible depuis w1 et w2 à la
fois).
Alors, dans le cas de S4 :
Théorème 3 [Correction, Complétude]
S4 est correcte et complète par rapport à la classe des cadres
réflexifs et transitifs.
Preuve : Que S4 soit correcte pour les cadres réflexifs et transitifs est
clair.
Pour prouver la complétude, et au lieu de montrer que |=
F implique |-S4 F (ou de façon équivalente,
|-S4F), nous allons supposer que non |-S4 F,
et montrer que non |=F.
Choisissons une formule F représentant le faux, c'est-à-dire
une formule qui implique toutes les autres prouvablement. Appelons
un ensemble de formules G cohérent s'il n'est pas
le cas que G |-S4 F. (De façon équivalente,
tel que F n'est pas faiblement déductible de G.) Si non
|-S4 F, alors ¬F est cohérent. En effet, si
nous avions ¬F|-S4F, alors nous aurions |-S4
¬ F Þ F, donc |-S4F par raisonnement
classique (c'est-à-dire sans utiliser aucune règle et aucun
axiome modaux).
Nous construisons maintenant un modèle de ¬F (un cadre et
une interprétation tels que ¬F soit vraie en un certain
monde). Définissons pour cela le cadre de Kripke (W,£), où
W est l'ensemble de tous les ensembles cohérents maximaux de
propositions de S4, et où w£ w' si et seulement si pout toute
formule de la forme  F' dans w, F' est dans w'.
Définissons enfin l'interprétation r par : pour chaque
variable A, r(A) est l'ensemble des mondes w tels que AÎ
w.
F' dans w, F' est dans w'.
Définissons enfin l'interprétation r par : pour chaque
variable A, r(A) est l'ensemble des mondes w tels que AÎ
w.
En premier, faisons quelques remarques sur les ensembles cohérents
maximaux w. Comme w est cohérent, il ne peut pas contenir à
la fois F et ¬ F, pour aucune formule F. Mais
pour toute formule F, w doit contenir soit F soit ¬
F. En effet, supposons que w ne contienne ni F ni ¬
F. Alors wÈ {F} et wÈ {¬ F} sont tous
les deux incohérents par maximalité de w, donc il existe un
ensemble fini de formules F1, ..., Fn dans
wÈ{F} tel que |-S4 F1 Þ ... Þ
Fn Þ F, et de même il existe un ensemble fini de
formules F'1, ..., F'n' dans wÈ{¬F}
tel que |-S4 F'1 Þ ... Þ F'n' Þ
F. Sans perte de généralité, supposons que F fait
partie des Fi (sinon nous l'y ajoutons), et en fait que F
= Fn, et de même nous pouvons supposer que ¬ F =
F'n'. Nous pouvons aussi supposer, en ajoutant suffisamment
de formules à chacun de ces deux ensembles, que les ensembles
{F1, ..., Fn-1} et {F'1, ...,
F'n'-1} coïncident. Alors on a |-S4 F1
Þ ... Þ Fn-1 Þ F Þ F et |-S4
F1 Þ ... Þ Fn-1 Þ ¬ F Þ F, donc
|-S4 F1 Þ ... Þ Fn-1 Þ (FÚ
¬ F) Þ F, mais ceci revient à dire que |-S4
F1 Þ ... Þ Fn-1 Þ F. De plus F1,
..., Fn-1 sont toutes dans w, donc w est
incohérent, ce qui est contradictoire. Donc w doit contenir
soit F soit ¬ F.
Observer aussi que tout ensemble cohérent maximal est stable par
déduction faible : si w est un ensemble cohérent maximal tel
que w|-S4 F, et si ¬ F était dans w, nous
pourrions déduire F de w en déduisant d'abord F, et en
utilisant ¬ F ensuite. Donc ¬ F Ï w, donc
F Î w.
Enfin, nous faisons la remarque que tout ensemble cohérent est
inclus dans un ensemble cohérent maximal. Pour le montrer, nous
utilisons le lemme de Zorn (une autre forme de l'axiome du choix),
qui énonce que tout ensemble ordonné inductif S a un
élément maximal. Rappelons qu'un ensemble est inductif
si et seulement si tout sous-ensemble totalement ordonné a une
borne supérieure. Dans notre cas, soit S l'ensemble de tous les
ensembles cohérents de formules, ordonnés par inclusion.
Étant donné un ensemble totalement ordonné d'ensemble
cohérents Ci, iÎ I, soit C = ÈiÎ I Ci. C
est cohérent, car sinon il existerait un nombre fini de formules
F1, ..., Fn dans C telles que |-S4 F1
Þ ... Þ Fn Þ F. Chaque Fi est dans un
certain Ci, et comme les Ci sont totalement ordonnés, il
existe un Ci contenant toutes les formules F1, ...,
Fn; mais alors Ci serait incohérent, ce qui est
contradictoire. Donc S est inductif et par le lemme de Zorn, on
peut compléter tout ensemble cohérent pour obtenir un ensemble
cohérent maximal.
Nous affirmons en premier que (W,£) est un cadre réflexif et
transitif, c'est-à-dire que £ est un pré-ordre. Il est en
effet réflexif, parce que pour tout  F'Î w, F' is
faiblement déductible de
F'Î w, F' is
faiblement déductible de  F' par modus ponens avec (T);
comme tout ensemble cohérent maximal est clos par
déductibilité faible, F'Î w. La relation £ est
aussi transitive : si w1£ w2£ w3, alors pour toute
formule
F' par modus ponens avec (T);
comme tout ensemble cohérent maximal est clos par
déductibilité faible, F'Î w. La relation £ est
aussi transitive : si w1£ w2£ w3, alors pour toute
formule  F'Î w1,
F'Î w1, 
 F'Î w1 par (4), donc
F'Î w1 par (4), donc
 F'Î w2 puisque w1£ w2, donc F'Î w3 vu que
w2£ w3; ceci entraîne w1£ w3.
F'Î w2 puisque w1£ w2, donc F'Î w3 vu que
w2£ w3; ceci entraîne w1£ w3.
Nous affirmons en second que pour toute formule F',
w,r|=F' si et seulement si F'Î w. Nous le
montrons par récurrence structurelle sur F' :
- Si F' est une variable, c'est une conséquence de la
définition de r.
- Si F' est de la forme F''ÚF''', alors : si
w,r |= F', alors w, r |= F'' ou w,r
|= F''', donc F'' ou F''' est dans w, par
hypothèse de récurrence; mais si F''Î w
(resp. F'''Î w), alors F'=F''ÚF''' est
faiblement déductible de w, donc F'Î w.
Réciproquement, si non w,r |=F', alors non w,r
|= F'' et non w,r |= F''', donc
F''Ï w et F'''Ï w par hypothèse de
récurrence; donc, par maximalité de w, ¬F'' et
¬F''' doivent être toutes les deux dans w, et donc les
formules faiblement déductibles ¬F''Ù¬F''' et
¬(F''ÚF''') (autrement dit ¬F') sont dans
w, et ainsi F' ne peut pas être dans w, par
cohérence.
- Le cas des conjonctions est similaire.
- Si F' est de la forme ¬F'', alors : si w,r
|= F', alors non w,r |= F'', donc par
hypothèse de récurrence F'' Ï w; en conséquence
F' = ¬F'' Î w. Réciproquement, si F'Î w,
alors F'' n'est pas dans w car sinon w ne serait pas
cohérent, donc par hypothèse de récurrence non w,r
|= F'', ce qui implique w,r|=F'.
- Si F' est de la forme
 F'', alors : si F'Î
w, alors F''Î w' pour tout w'³ w par définition de
£, donc par hypothèse de récurrence
w',r|=F'' pour tout w'³ w, ce qui implique
w,r|=F'.
F'', alors : si F'Î
w, alors F''Î w' pour tout w'³ w par définition de
£, donc par hypothèse de récurrence
w',r|=F'' pour tout w'³ w, ce qui implique
w,r|=F'.
Réciproquement, si w,r|=F', alors w',r |=
F'' pour tout w'³ w, donc par hypothèse de récurrence
F''Î w' pour tout w'³ w. Maintenant, considérons
l'ensemble w'0 = {Y |  Y Î w}.
Y Î w}.
Nous affirmons que w'0 È {¬F''} est incohérent.
En effet, supposons le contraire, autrement dit supposons que
w'0È{¬F''} est cohérent. Complétons-le pour
former un sur-ensemble cohérent maximal w'1. Par
définition de w'0, de w'1 et de £, w£ w'1.
Comme F''Î w' pour tout w'³ w, nous devons donc avoir
F'' Î w'1. Mais alors w'1 contient à la fois
F'' et ¬F'' (par construction), et est donc
incohérent.
Donc w'0È{¬F''} est incohérent, et nous pouvons
faiblement déduire F de w'0, ¬F'', donc par
raisonnement classique nous pouvons dériver F'' de w'0.
(Observer que la déduction faible satisfait le théorème de
la déduction par définition.) Mais alors, il existe un nombre
fini de formules Y1, ..., Yn dans w'0 telles
que |-S4 Y1 Þ ... Þ Yn Þ F''.
Donc |-S4  (Y1 Þ ... Þ Yn Þ
F'') par (Nec), donc |-S4
(Y1 Þ ... Þ Yn Þ
F'') par (Nec), donc |-S4 Y1Þ ...Þ
Y1Þ ...Þ
 YnÞ
YnÞ  F'' par n applications de l'axiome (K)
et le raisonnement classique. Il s'ensuit que
F'' par n applications de l'axiome (K)
et le raisonnement classique. Il s'ensuit que  F'',
c'est-à-dire F', est faiblement déductible à partir de
F'',
c'est-à-dire F', est faiblement déductible à partir de
 Yi, 1£ i£ n, qui sont toutes dans w par
construction. Donc F' est elle-même dans w.
Yi, 1£ i£ n, qui sont toutes dans w par
construction. Donc F' est elle-même dans w.
Finalement, comme ¬F est cohérent, on peut compléter
{¬ F} pour former un ensemble cohérent maximal w, et
par définition de W, £ et r, ceci implique que w,r
|= ¬F.
¤
Ce théorème signifie que F est prouvable en S4 si et
seulement si elle est vraie dans tout cadre dont la relation
d'accessibilité est un pré-ordre. En fait, on peut se restreindre
aux cadres où la relation d'accessbilité est un ordre,
c'est-à-dire où elle est aussi anti-symétrique. (C'est parce
que les modèles définis par filtration ci-dessous seront
anti-symétriques.)
Bien que nous n'ayons prouvé le théorème que pour S4, des
théorèmes analogues peuvent être prouvés pour les autres
logiques. Par exemple, KD est correct et complet pour tous les cadres
séquentiels, S pour les cadres réflexifs, K4 pour les cadres
transitifs, S5 pour toutes les relations d'équivalence
(réflexives, symétriques, transitives), et S4.2 pour tous les
pré-ordres convergents. La preuve est exactement la même que
ci-dessus. En particulier, nous construisons la relation
d'accessibilité £ en disant que w£ w' si et seulement si
pour toute formule  Y dans w, Y est dans w'. La
seule différence est que £ sera quelque chose d'autre : une
relation séquentielle pour KD, une relation réflexive pour S, etc.
Y dans w, Y est dans w'. La
seule différence est que £ sera quelque chose d'autre : une
relation séquentielle pour KD, une relation réflexive pour S, etc.
2.4 Décidabilité
Pour nous aider à montrer qu'une logique modale L est décidable,
définissons une relation d'équivalence sur les mondes (une
relation d'indistingabilité) et le quotient des cadres par cette
relation. Cette définition est justifiée par la construction du
théorème 7.
Définition 4 [Filtration] Soit F une formule de L, et r une affectation. Soit
S(F) l'ensemble des sous-formules de F.
La relation d'indistingabilité ºF, r sur
un cadre (W,R) est définie par wºF, r w' si et
seulement si pour toute formule F'Î S(F),
w,r|=F' si et seulement si w',r|=F'.
La filtration de (W,R) par S(F),r est le cadre
(W/Fr, R/Fr), où W/Fr est le quotient de W
par ºF, r et si v, v' sont deux éléments
de W/Fr, alors v(R/Fr) v' si et seulement s'il
existe wÎ v, w'Î v' tels que w R w'.
Soit wF,r la classe de w modulo ºF,
r, et soit rF l'affectation dans (W/Fr,
R/Fr) qui envoie chaque variable A vers le quotient
r(A)/Fr = {wF,r | wÎr(A)}.
La relation ºF est en effet une relation
d'équivalence sur les mondes. La filtration préserve les
modèles :
Lemme 5
Pour toute sous-formule F' de F, (W,R,r) |=
F' si et seulement si (W/Fr, R/Fr, rF)
|= F'.
Preuve : Nous affirmons que : (1) si vÎ W/Fr, alors
v,rF|=F' si et seulement si l'une des deux
conditions équivalentes suivantes est vérifiée :
- il y a un wÎ W tel que v=wF,r et
w,r|=F';
- pour tout wÎ W tel que v=wF,r, alors
w,r|=F'.
Ces conditions sont équivalentes; en effet, 2 implique 1 parce que
les classes d'équivalence sont non vides, et 1 implique 2 parce
que les mondes d'une même classe d'équivalence sont
indistingables et parce que F' est une sous-formule de F.
L'affirmation (1) est alors montrée par récurrence structurelle
sur F'.
En guise d'illustration, traitons le cas où F' est de la
forme  F''. Si v, rF|=
F''. Si v, rF|=  F'', alors
pour tout v' tel que v(R/Fr)v', v', rF |=F'' est vrai; donc, pour tout wÎ v, pour tout w'
tel que w R w', w'/Fr, rF|=F'' par
définition de R/Fr; par hypothèse de récurrence,
w',r|=F'' pour tous ces w', donc w, r |=
F'', alors
pour tout v' tel que v(R/Fr)v', v', rF |=F'' est vrai; donc, pour tout wÎ v, pour tout w'
tel que w R w', w'/Fr, rF|=F'' par
définition de R/Fr; par hypothèse de récurrence,
w',r|=F'' pour tous ces w', donc w, r |=
 F''. Réciproquement, si pour tout wÎ v, w, r
|=
F''. Réciproquement, si pour tout wÎ v, w, r
|=  F'', alors pour tout w' tel que w R w', w',
r |=F''; donc pour tout v' tel que v(R/Fr)v',
il y a un wÎ v et un w'Î v' tels que w R w', d'où w',
r |=F'', et par hypothèse de récurrence, v',
rF |=F''; comme v' est arbitraire, il s'ensuit
que v, rhoF |=
F'', alors pour tout w' tel que w R w', w',
r |=F''; donc pour tout v' tel que v(R/Fr)v',
il y a un wÎ v et un w'Î v' tels que w R w', d'où w',
r |=F'', et par hypothèse de récurrence, v',
rF |=F''; comme v' est arbitraire, il s'ensuit
que v, rhoF |= F''.
¤
F''.
¤
De plus, la filtration préserve la plupart des propriétés du
modèle :
Lemme 6
Si (W,R) est réflexif (resp. symétrique, séquentiel),
alors (W/Fr, R/Fr) est réflexif
(resp. symétrique, séquentiel).
Preuve : Si (W,R) est réflexif, alors pour tout vÎ W/Fr, il
existe un monde wÎ v, et w R w par hypothèse, donc
v(R/Fr)v par définition.
Si (W,R) est symétrique, et v(R/Fr)v', alors il existe
w,w'Î W tels que w R w', donc w' R w par symétrie, et
donc v'(R/Fr)v.
Si (W,R) est séquentiel, alors pour tout vÎ W/Fr, il y
a un w dans v, et aussi un w'Î W tel que w R w' par
hypothèse, donc v(R/Fr)w'/Fr, et
(W/Fr,R/Fr) est séquentiel.
¤
Cependant, quand (W,R) est transitif, (W/Fr, R/Fr) ne
l'est pas nécessairement. En effet, si v(R/ Fr)v' et v'(R/
Fr)v'', alors il existe des mondes w, w'1, w'2, w''
tels que w R w'1 et w'2 R w'', mais on ne peut rien en
conclure, car il n'y a pas nécessairement de relation entre w'1
et w'2. De même, quand (W,R) est convergent, (W/Fr,
R/Fr) n'est pas nécessairement convergent. Nous réglerons
ce problème bientôt.
Finalement, la filtration est suffisamment petite :
Théorème 7 [Petit modèle]
Soit F une formule de taille n. Le cardinal de W/Fr
est inférieur ou égal à 2n.
Preuve : Pour tout F'Î S(F), soit f0(F') = {wÎ W| w,r
|= F'}, et f1(F') = {wÎ W| non w,r |=
F'}.
Maintenant, soient F1, ..., Fn les n sous-formules
de F, et soit s1, ..., sn une suite arbitraire
d'éléments de {0,1}. Alors Çi=1n
fsi(Fi) est une classe d'équivalence modulo
ºF,r, c'est-à-dire un élément de
W/Fr.
Réciproquement, toute classe d'équivalence est déterminée
par la valeur booléenne (vrai si si=0, faux si si=1) de
toutes les sous-formules Fi, 1£ i£ n, de F.
Autrement dit toutes les classes d'équivalence sont de la forme
Çi=1n fsi(Fi) pour une certaine suite s1,
..., sn.
Il y a donc au plus autant de mondes dans W/Fr qu'il n'y a
de suites de longueur n sur {0,1}, soit au plus 2n.
¤
Ceci établit la propriété dite de petit modèle pour
toutes les logiques pour lesquelles (W/Fr, R/Fr,
rF) est un modèle de F dès que (W,R,r) en
est un. Ceci fonctionne pour toute combinaison de réflexivité, de
symétrie et de séquentialité.
Lorsque les modèles sont transitifs, (W/Fr, R/Fr,
rF) peut ne pas être un modèle de F du tout bien
que (W,R,r) en soit un. Dans ce cas, nous remplaçons le
lemme 5 par :
Lemme 8
Supposons R transitive.
Pour toute sous-formule F' de F, (W,R,r) |=
F' si et seulement si (W/Fr, (R/Fr)+,
rF)|=F', où (R/Fr)+ est la clôture
transitive de R/Fr.
Preuve : Comme pour le lemme 5.
¤
Quand R est transitive, donc, si (W,R,r) est un modèle de
F, alors (W/Fr, (R/Fr)+, rF) est un autre
modèle de F, qui est clairement petit (fini). Une technique
analogue fonctionne pour les cadres de Kripke convergents
(resp. convergents et transitifs).
Ce qui fait que la propriété de petit modèle est utile est :
Théorème 9 [Décidabilité] Soit L une logique modale ayant la propriété de petit
modèle. Alors la validité des formules F de L est
décidable.
Preuve : Soit n la taille de F, et supposons que la taille d'un petit
modèle pour F est majorée par f(n). (Nous avions
f(n)=O(2n) plus haut.) Énumérons tous les graphes ayant au
plus f(n) sommets et qui sont dans la classe C. Pour ce
faire, nous énumérons tous les graphes ayant exactement m
sommets, pour tout 1£ m£ f(n) : il suffit d'énumérer
tous les graphes sur {1,...,m}, et il y en a au plus
2m2. Sur un graphe à m sommets, il y a au plus 2nm
affectations possibles (associant chaque variable et monde à un
booléen disant si le variable est vrai à ce monde ou non), et
nous vérifions chaque affectation en temps O(nm) (calculant la
valeur de vérité de chaque sous-formule en chaque monde, en
partant des formules atomiques et en remontant dans F). En
somme, le temps d'exécution est majoré par
O(Sm=1f(n) 2m2. 2nm. nm) £ nf(n)2.
2f(n)2+nf(n).
¤
Ceci est le cas, comme nous l'avons vu, des classes de cadres
satisfaisant n'importe quelle combinaison de réflexivité, de
symétrie, de transitivité, de séquentialité et de convergence.
- En jargon de théorie de la complexité, la borne supérieure du
temps que prend l'algorithme de petit modèle ci-dessus est dite
doublement exponentielle. Si l'on examine l'algorithme plus
attentivement, nous voyons que déterminer si F est invalide
demande de deviner un cadre et une affectation dans ce cadre en
temps simplement exponentiel, et de les vérifier en temps
simplement exponentiel. En somme, l'algorithme tourne en temps
non déterministe simplement exponentiel. Cependant, la plupart
des logiques modales sont décidables en temps déterministe
simplement exponentiel, ce qui est beaucoup moins intractable,
quoique toujours prouvablement intractable (autrement dit,
certainement pas faisable en temps polynomial dans tous les cas).
Le problème de la satisfiabilité dans la plupart de ces
logiques, comme S4, est en fait PSPACE-complet, et pour S5 il n'est
même ``que'' NP-complet.
- L'astuce qui fait que la propriété de petit modèle fonctionne
est de considérer une relation d'indistingabilité définie sur
l'ensemble S(F) de toutes les sous-formules de F. C'est
une façon sémantique de dire que la sémantique de F ne
dépend que de ses sous-formules, et c'est donc une version
analogue de la propriété de sous-formule que l'on dérive
usuellement comme une conséquence du processus syntaxique
d'élimination des coupures.
2.5 Systèmes de séquents et tableaux
Melvin Fitting [Fit83] a été l'un des
premiers logiciens à s'intéresser aux systèmes de preuve pour
les logiques modales. Il s'avère que la plupart des méthodes de
preuve connues pour la logique classique ne s'adaptent pas au logiques
modales. Cependant, les méthodes de tableaux, à savoir les
systèmes de séquents de Gentzen sans coupures, ont beaucoup de
succès dans ce domaine. (Pour une autre méthode,
voir [Ohl93].)
Mais l'élimination des coupures ou la propriété de sous-formule
échoue dans certaines logiques modales. S4R [Gor91],
par exemple, a un système de séquents sans coupures, mais qui n'a
pas la propriété de sous-formule : on peut avoir besoin de
sous-formules non seulement de F, mais aussi de  F
pendant la recherche de preuve. Ce n'est pas trop grave, puisque la
décidabilité est conservée. Des logiques comme S4.2 et S4F ont
des systèmes de Gentzen qui non seulement n'ont pas la propriété
de sous-formule (on doit considérer toutes les sous-formules de
F
pendant la recherche de preuve. Ce n'est pas trop grave, puisque la
décidabilité est conservée. Des logiques comme S4.2 et S4F ont
des systèmes de Gentzen qui non seulement n'ont pas la propriété
de sous-formule (on doit considérer toutes les sous-formules de
 ¬
¬ F), mais exigent aussi des règles dites de coupures analytiques. Cette forme spéciale de la règle Cut est
telle que la formule de coupure (celle qui disparaît dans la
conclusion de Cut) est toujours une sous-formule directe de l'une des
formules dans la conclusion de la règle Cut, ce qui limite
l'explosion de l'espace de recherche; la décidabilité est encore
préservée, mais à un prix élevé.
F), mais exigent aussi des règles dites de coupures analytiques. Cette forme spéciale de la règle Cut est
telle que la formule de coupure (celle qui disparaît dans la
conclusion de Cut) est toujours une sous-formule directe de l'une des
formules dans la conclusion de la règle Cut, ce qui limite
l'explosion de l'espace de recherche; la décidabilité est encore
préservée, mais à un prix élevé.
Examinons quelques exemples concrets. Un système de séquents
dérivé de ce que Goré propose pour S4 est LK0 sans Cut plus
les règles :

où, si G est un ensemble de formules,  G est
l'ensemble {
G est
l'ensemble { Y|YÎG}.
Y|YÎG}.
Interprétons ces règles comme des règles de tableaux. Supposons
que nous soyons sur un chemin non clos. Les formules de type a
et b s'expansent comme dans le cas classique. Mais si nous
décidons d'expanser une formule de la forme + F, nous devons
le faire en la remplaçant sur le chemin courant par +F, et
nous devons aussi masquer toutes les formules négatives -Y
telles que Y n'est pas de la forme
F, nous devons
le faire en la remplaçant sur le chemin courant par +F, et
nous devons aussi masquer toutes les formules négatives -Y
telles que Y n'est pas de la forme  Y', ainsi que toutes
les formules positives sauf F (règle (S4)). Et, si nous
souhaitons expanser une formule de la forme -
Y', ainsi que toutes
les formules positives sauf F (règle (S4)). Et, si nous
souhaitons expanser une formule de la forme - F, nous devons
le faire en ajoutant -F sur le chemin. (La contraction implicite
à gauche des séquents dans la règle (T) n'est pas
éliminable.)
F, nous devons
le faire en ajoutant -F sur le chemin. (La contraction implicite
à gauche des séquents dans la règle (T) n'est pas
éliminable.)
Remarquer que, contrairement à la logique classique, nous ne pouvons
pas choisir de décomposer n'importe quelle formule arbitraire sur le
chemin : si nous décomposons une formule + F en utilisant
(S4), nous ne pourrons plus accéder aux formules de G' ou
D, et il faudra que nous rebroussions chemin (``backtrack'' en
anglais), que nous choisissions une autre formule à décomposer si
la première n'a mené à rien. À cause de règles comme (S4),
les tableaux pour les logiques modales ne sont pas aussi simples que
dans le cas classique.
F en utilisant
(S4), nous ne pourrons plus accéder aux formules de G' ou
D, et il faudra que nous rebroussions chemin (``backtrack'' en
anglais), que nous choisissions une autre formule à décomposer si
la première n'a mené à rien. À cause de règles comme (S4),
les tableaux pour les logiques modales ne sont pas aussi simples que
dans le cas classique.
D'autres logiques modales ont des systèmes de séquents beaucoup
plus compliqués que S4, pourtant. Par exemple, voici une variante
du système de Goré pour S4.2. En plus des règles de LK0
(sans Cut), des règles (T) et (S4) ci-dessus, nous incluons :

où (...)* est appelée une formule marquée, et la règle
est restreinte au cas où  F n'est pas marquée dans la
conclusion. (Les marques sont juste des annotations sur des
occurrences de formules, et ne participent pas de la structure de la
formule; leur rôle est de détecter les bouclages, c'est-à-dire
les situations où une même règle devrait être appliquée deux
fois à la même formule.) Pour trouver une preuve en S4.2, lorsque
nous en arrivons à expanser une formule de la forme +
F n'est pas marquée dans la
conclusion. (Les marques sont juste des annotations sur des
occurrences de formules, et ne participent pas de la structure de la
formule; leur rôle est de détecter les bouclages, c'est-à-dire
les situations où une même règle devrait être appliquée deux
fois à la même formule.) Pour trouver une preuve en S4.2, lorsque
nous en arrivons à expanser une formule de la forme + F,
nous avons le choix entre appliquer la règle (S4) ou la règle
(K45); cette dernière enrichit le chemin courant, et produit deux
chemins sur lesquels (S4) produira des séquents plus riches en
information.
F,
nous avons le choix entre appliquer la règle (S4) ou la règle
(K45); cette dernière enrichit le chemin courant, et produit deux
chemins sur lesquels (S4) produira des séquents plus riches en
information.
Mais la règle (S4.2) ne suffit pas à trouver toutes les preuves,
et nous devons ajouter les règles de coupures analytiques
suivantes :
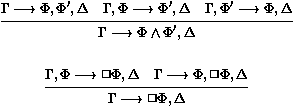
ainsi que les règles correspondantes pour Ú et les
autres conncteurs. (Goré n'utilise que ¬, Ù et  comme
connecteurs de base.) Ces règles rajoute beaucoup de non-déterminisme
et de branchement dans la recherche de preuve : trouver des preuves
dans ces logiques n'est pas facile.
comme
connecteurs de base.) Ces règles rajoute beaucoup de non-déterminisme
et de branchement dans la recherche de preuve : trouver des preuves
dans ces logiques n'est pas facile.



 (FÞ F')Þ
(FÞ F')Þ FÞ
FÞ F'
F'
 FÞ F
FÞ F
 FÞ
FÞ 
 F
F



 : si F est une formule, alors
: si F est une formule, alors  F est une formule
aussi (``box F'', ou ``nécessairement, F''; en termes
temporels, ``dans tout futur, F''). Nous supposons que
F est une formule
aussi (``box F'', ou ``nécessairement, F''; en termes
temporels, ``dans tout futur, F''). Nous supposons que  a
une priorité plus forte que tous les autres opérateurs logiques,
de sorte que
a
une priorité plus forte que tous les autres opérateurs logiques,
de sorte que  AÞ A est une abréviation de (
AÞ A est une abréviation de ( A)Þ
A, par exemple. Nous définissons aussi à F comme une
abréviation de ¬
A)Þ
A, par exemple. Nous définissons aussi à F comme une
abréviation de ¬ ¬ F (``possiblement, A''; en termes
temporels, ``à un moment dans un futur, A'').
¬ F (``possiblement, A''; en termes
temporels, ``à un moment dans un futur, A''). (FÞ F')Þ
(FÞ F')Þ FÞ
FÞ F'
F'
 FÞ F
FÞ F
 FÞ
FÞ 
 F
F
 F, pour chaque formule F.
F, pour chaque formule F.
 comme un opérateur
de futur, (4) exprime la transitivité du temps, c'est-à-dire que
si F est vraie dans tous les futurs, alors elle est aussi vraie
dans tous les futurs de tous ces futurs.
comme un opérateur
de futur, (4) exprime la transitivité du temps, c'est-à-dire que
si F est vraie dans tous les futurs, alors elle est aussi vraie
dans tous les futurs de tous ces futurs. àF,
àF,
 FÞàF,
FÞàF,
 FÞ(FÞ
FÞ(FÞ F),
F),
 FÞF')Ú(à
FÞF')Ú(à F'ÞF),
F'ÞF),
 FÞ
FÞ àF
àF
A se lit ``on croit que A'' ou ``on sait A''. Étant donnée une logique modale S (monotone) et un ensemble de formules G, la formule A est une conséquence monotone de G dans S si elle est déductible dans S à partir de G, ce que l'on écrit usuellement G |-S A. L'ensemble G est habituellement appelé une théorie et les conséquences monotones de G dans S sont les formules déductibles de G dans S; c'est-à-dire CnS(G) = {A| G |-S A}. Le système est ``monotone'' en ce sens que si A est dans CnS(G), alors elle sera dans CnS(G') pour tout sur-ensemble G' de G.
A (``on ne sait pas A'') s'il n'y a pas de déduction de A dans S à partir de G et des hypothèses précédentes. Plus formellement, la théorie T est une S-expansion de la théorie G si elle satisfait l'équation T = CnS(G È {¬
A | A Ï T}). Comme T apparaît sur le côté droit, la définition est circulaire, et conséquemment, une théorie G peut avoir zéro, une ou plusieurs S-expansions. Pour contre-balancer ce phénomène, l'ensemble des conséquences non monotones de G dans S est usuellement défini comme l'intersection de toutes les S-expansions de G. Le nouveau système est ``non-monotone'' parce que, bien que A puisse être une conséquence non monotone de G, elle peut ne pas être une conséquence non monotone d'un sur-ensemble de G.
 F est vraie dans un monde w
si et seulement si F est vraie dans tous les mondes qui le
suivent (à tous les instants ultérieurs).
F est vraie dans un monde w
si et seulement si F est vraie dans tous les mondes qui le
suivent (à tous les instants ultérieurs). F si et seulement si pour tout monde
w' tel que w R w', alors w'|=F.
F si et seulement si pour tout monde
w' tel que w R w', alors w'|=F.
 F' dans w, F' est dans w'.
Définissons enfin l'interprétation r par : pour chaque
variable A, r(A) est l'ensemble des mondes w tels que AÎ
w.
F' dans w, F' est dans w'.
Définissons enfin l'interprétation r par : pour chaque
variable A, r(A) est l'ensemble des mondes w tels que AÎ
w. F'Î w, F' is
faiblement déductible de
F'Î w, F' is
faiblement déductible de  F' par modus ponens avec (T);
comme tout ensemble cohérent maximal est clos par
déductibilité faible, F'Î w. La relation £ est
aussi transitive : si w1£ w2£ w3, alors pour toute
formule
F' par modus ponens avec (T);
comme tout ensemble cohérent maximal est clos par
déductibilité faible, F'Î w. La relation £ est
aussi transitive : si w1£ w2£ w3, alors pour toute
formule  F'Î w1,
F'Î w1, 
 F'Î w1 par (4), donc
F'Î w1 par (4), donc
 F'Î w2 puisque w1£ w2, donc F'Î w3 vu que
w2£ w3; ceci entraîne w1£ w3.
F'Î w2 puisque w1£ w2, donc F'Î w3 vu que
w2£ w3; ceci entraîne w1£ w3. F'', alors : si F'Î
w, alors F''Î w' pour tout w'³ w par définition de
£, donc par hypothèse de récurrence
w',r|=F'' pour tout w'³ w, ce qui implique
w,r|=F'.
F'', alors : si F'Î
w, alors F''Î w' pour tout w'³ w par définition de
£, donc par hypothèse de récurrence
w',r|=F'' pour tout w'³ w, ce qui implique
w,r|=F'. Y Î w}.
Y Î w}. (Y1 Þ ... Þ Yn Þ
F'') par (Nec), donc |-S4
(Y1 Þ ... Þ Yn Þ
F'') par (Nec), donc |-S4 Y1Þ ...Þ
Y1Þ ...Þ
 YnÞ
YnÞ  F'' par n applications de l'axiome (K)
et le raisonnement classique. Il s'ensuit que
F'' par n applications de l'axiome (K)
et le raisonnement classique. Il s'ensuit que  F'',
c'est-à-dire F', est faiblement déductible à partir de
F'',
c'est-à-dire F', est faiblement déductible à partir de
 Yi, 1£ i£ n, qui sont toutes dans w par
construction. Donc F' est elle-même dans w.
Yi, 1£ i£ n, qui sont toutes dans w par
construction. Donc F' est elle-même dans w.
 Y dans w, Y est dans w'. La
seule différence est que £ sera quelque chose d'autre : une
relation séquentielle pour KD, une relation réflexive pour S, etc.
Y dans w, Y est dans w'. La
seule différence est que £ sera quelque chose d'autre : une
relation séquentielle pour KD, une relation réflexive pour S, etc. F''. Si v, rF|=
F''. Si v, rF|=  F'', alors
pour tout v' tel que v(R/Fr)v', v', rF |=F'' est vrai; donc, pour tout wÎ v, pour tout w'
tel que w R w', w'/Fr, rF|=F'' par
définition de R/Fr; par hypothèse de récurrence,
w',r|=F'' pour tous ces w', donc w, r |=
F'', alors
pour tout v' tel que v(R/Fr)v', v', rF |=F'' est vrai; donc, pour tout wÎ v, pour tout w'
tel que w R w', w'/Fr, rF|=F'' par
définition de R/Fr; par hypothèse de récurrence,
w',r|=F'' pour tous ces w', donc w, r |=
 F''. Réciproquement, si pour tout wÎ v, w, r
|=
F''. Réciproquement, si pour tout wÎ v, w, r
|=  F'', alors pour tout w' tel que w R w', w',
r |=F''; donc pour tout v' tel que v(R/Fr)v',
il y a un wÎ v et un w'Î v' tels que w R w', d'où w',
r |=F'', et par hypothèse de récurrence, v',
rF |=F''; comme v' est arbitraire, il s'ensuit
que v, rhoF |=
F'', alors pour tout w' tel que w R w', w',
r |=F''; donc pour tout v' tel que v(R/Fr)v',
il y a un wÎ v et un w'Î v' tels que w R w', d'où w',
r |=F'', et par hypothèse de récurrence, v',
rF |=F''; comme v' est arbitraire, il s'ensuit
que v, rhoF |= F''.
¤
F''.
¤ F
pendant la recherche de preuve. Ce n'est pas trop grave, puisque la
décidabilité est conservée. Des logiques comme S4.2 et S4F ont
des systèmes de Gentzen qui non seulement n'ont pas la propriété
de sous-formule (on doit considérer toutes les sous-formules de
F
pendant la recherche de preuve. Ce n'est pas trop grave, puisque la
décidabilité est conservée. Des logiques comme S4.2 et S4F ont
des systèmes de Gentzen qui non seulement n'ont pas la propriété
de sous-formule (on doit considérer toutes les sous-formules de
 ¬
¬ F), mais exigent aussi des règles dites de coupures analytiques. Cette forme spéciale de la règle Cut est
telle que la formule de coupure (celle qui disparaît dans la
conclusion de Cut) est toujours une sous-formule directe de l'une des
formules dans la conclusion de la règle Cut, ce qui limite
l'explosion de l'espace de recherche; la décidabilité est encore
préservée, mais à un prix élevé.
F), mais exigent aussi des règles dites de coupures analytiques. Cette forme spéciale de la règle Cut est
telle que la formule de coupure (celle qui disparaît dans la
conclusion de Cut) est toujours une sous-formule directe de l'une des
formules dans la conclusion de la règle Cut, ce qui limite
l'explosion de l'espace de recherche; la décidabilité est encore
préservée, mais à un prix élevé.
 G est
l'ensemble {
G est
l'ensemble { Y|YÎG}.
Y|YÎG}. F, nous devons
le faire en la remplaçant sur le chemin courant par +F, et
nous devons aussi masquer toutes les formules négatives -Y
telles que Y n'est pas de la forme
F, nous devons
le faire en la remplaçant sur le chemin courant par +F, et
nous devons aussi masquer toutes les formules négatives -Y
telles que Y n'est pas de la forme  Y', ainsi que toutes
les formules positives sauf F (règle (S4)). Et, si nous
souhaitons expanser une formule de la forme -
Y', ainsi que toutes
les formules positives sauf F (règle (S4)). Et, si nous
souhaitons expanser une formule de la forme - F, nous devons
le faire en ajoutant -F sur le chemin. (La contraction implicite
à gauche des séquents dans la règle (T) n'est pas
éliminable.)
F, nous devons
le faire en ajoutant -F sur le chemin. (La contraction implicite
à gauche des séquents dans la règle (T) n'est pas
éliminable.) F en utilisant
(S4), nous ne pourrons plus accéder aux formules de G' ou
D, et il faudra que nous rebroussions chemin (``backtrack'' en
anglais), que nous choisissions une autre formule à décomposer si
la première n'a mené à rien. À cause de règles comme (S4),
les tableaux pour les logiques modales ne sont pas aussi simples que
dans le cas classique.
F en utilisant
(S4), nous ne pourrons plus accéder aux formules de G' ou
D, et il faudra que nous rebroussions chemin (``backtrack'' en
anglais), que nous choisissions une autre formule à décomposer si
la première n'a mené à rien. À cause de règles comme (S4),
les tableaux pour les logiques modales ne sont pas aussi simples que
dans le cas classique.
 F n'est pas marquée dans la
conclusion. (Les marques sont juste des annotations sur des
occurrences de formules, et ne participent pas de la structure de la
formule; leur rôle est de détecter les bouclages, c'est-à-dire
les situations où une même règle devrait être appliquée deux
fois à la même formule.) Pour trouver une preuve en S4.2, lorsque
nous en arrivons à expanser une formule de la forme +
F n'est pas marquée dans la
conclusion. (Les marques sont juste des annotations sur des
occurrences de formules, et ne participent pas de la structure de la
formule; leur rôle est de détecter les bouclages, c'est-à-dire
les situations où une même règle devrait être appliquée deux
fois à la même formule.) Pour trouver une preuve en S4.2, lorsque
nous en arrivons à expanser une formule de la forme + F,
nous avons le choix entre appliquer la règle (S4) ou la règle
(K45); cette dernière enrichit le chemin courant, et produit deux
chemins sur lesquels (S4) produira des séquents plus riches en
information.
F,
nous avons le choix entre appliquer la règle (S4) ou la règle
(K45); cette dernière enrichit le chemin courant, et produit deux
chemins sur lesquels (S4) produira des séquents plus riches en
information.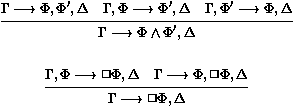
 comme
connecteurs de base.) Ces règles rajoute beaucoup de non-déterminisme
et de branchement dans la recherche de preuve : trouver des preuves
dans ces logiques n'est pas facile.
comme
connecteurs de base.) Ces règles rajoute beaucoup de non-déterminisme
et de branchement dans la recherche de preuve : trouver des preuves
dans ces logiques n'est pas facile.

